⭐️ 난이도
Gold 4
⭐️ 문제
https://www.acmicpc.net/problem/1707
1707번: 이분 그래프
입력은 여러 개의 테스트 케이스로 구성되어 있는데, 첫째 줄에 테스트 케이스의 개수 K가 주어진다. 각 테스트 케이스의 첫째 줄에는 그래프의 정점의 개수 V와 간선의 개수 E가 빈 칸을 사이에
www.acmicpc.net
⭐️ Idea flow
이분 그래프 기본 문제였다.
각 테스트 케이스마다 주어진 그래프에 대해서, 해당 그래프의 이분 그래프 여부를 구하는 문제이다.
따라서 이분 그래프에 대해서 알고 있으면 풀 수 있는 문제였다.
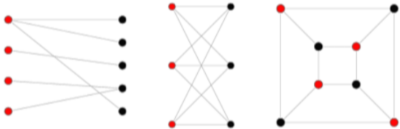
이분 그래프란 인접한 정점끼리 서로 다른 색으로 칠하여 모든 정점을 두 그룹으로 나누고, 서로 다른 그룹의 정점을 간선으로 연결한 그래프를 말한다.
이분 그래프의 여부를 확인하는 방법에는 BFS와 DFS 모두 사용할 수 있는데, 두 방법 모두 결과적으로는
"모든 인접한 정점이 서로 다른 색으로 칠해지면 이분 그래프"이고, 그렇지 않으면 이분 그래프가 아니다.
[전체적인 알고리즘]
1. 입력을 받으면서 정점 간에 간선을 양방향으로 연결해준다.
2. DFS를 통해서 정점의 색을 칠해준다.
2-1. 이 때, 정점을 아직 방문하지 않았다면 RED(빨간색)으로 칠해주고,
2-2. 현재 방문하고 있는 정점과 인접해있는 정점의 색을 현재 색과 다른 색으로 칠해준다.
3. 정점에 색을 칠하는 과정이 끝나면, 모든 정점에 대해서 연결되어 있는 정점들을 검사하면서
3-1. 만일 색이 같다면 그 즉시 false를 반환하고 (이분 그래프 X)
3-2. 모든 정점을 검사했는데 3-1과 같은 경우가 끝까지 없었다면 true를 반환한다. (이분 그래프 O)
⭐️ Code
#include <iostream>
#include <algorithm>
#include <string>
#include <cstring>
#include <cmath>
#include <vector>
#define INF 987654321;
#define RED 1
#define BLUE 2
using namespace std;
// 1707 - 이분 그래프
int v, e;
vector<vector<int>> graph;
vector<int> isVisited;
void input(){
cin >> v >> e;
graph.assign(v + 1, vector<int>(0, 0));
isVisited.assign(v + 1, false);
for(int i = 0; i < e; i++){
int s, e;
cin >> s >> e;
graph[s].emplace_back(e);
graph[e].emplace_back(s);
}
}
void DFS(int cur){
// 아직 방문하지 않은 정점이라면 빨간색으로 칠한다.
if(!isVisited[cur]) isVisited[cur] = RED;
// 현재 정점과 연결된 정점들을 모두 방문
for(int i = 0; i < graph[cur].size(); i++){
int next = graph[cur][i];
// 아직 방문하지 않은 정점이라면 현재 정점과 반대되는 색으로 칠한다.
if(!isVisited[next]){
if(isVisited[cur] == RED) isVisited[next] = BLUE;
else if(isVisited[cur] == BLUE) isVisited[next] = RED;
DFS(next);
}
}
}
// 이분 그래프인지 확인하는 함수
bool isBipartite(){
// 모든 정점들을 돌아보면서 인접한 정점과의 색이 같은지 확인
for(int cur = 1; cur <= v; cur++){
for(int i = 0; i < graph[cur].size(); i++){
int next = graph[cur][i];
// 만일 인접한 정점과 색이 같다면 이분 그래프가 아님
if(isVisited[cur] == isVisited[next]) return false;
}
}
return true;
}
int main(){
ios::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
int testcase;
cin >> testcase;
while(testcase--){
input();
// 그래프가 모두 연결되어 있다는 보장이 없으니, 방문 처리가 되지 않은 정점들에 DFS 실행
for(int i = 1; i <= v; i++){
if(!isVisited[i]) DFS(i);
}
if(isBipartite()) cout << "YES\n";
else cout << "NO\n";
}
return 0;
}
