[백준 2056 C++][G4] 작업

⭐️ 난이도

 

Gold 4

---

⭐️ 문제

https://www.acmicpc.net/problem/2056

2056번: 작업

 

 

---

⭐️ Idea flow

 

 

문제를 읽어보면 각각의 작업들에 대해 해당 작업에 걸리는 시간과 선행 관계에 있는 작업들의 번호들이 주어진다.

이는 곧 일에 따른 순서가 정해져 있다는 뜻이고, 이러한 경우에는 위상 정렬(Topology sort)이 적절하다.

 

하지만 이 문제는 기본적인 위상 정렬 문제 처럼 방문 순서를 구하는 것이 아니라, 제일 마지막 작업을 완료하는데까지 걸리는 최소 시간을 구해야 한다.

 

 

[처음 생각한 풀이 - 오답]

위상 정렬은 queue를 이용해서 풀어야하는 문제이고, queue는 level 별로 확인할 수 있다는 장점이 있다.

이를 이용하는 방법을 생각해냈는데, 같은 레벨에 있다는 이야기는 다음 작업으로 넘어가기 전에 수행해야 하는 작업이라는 뜻이다.

문제 예시

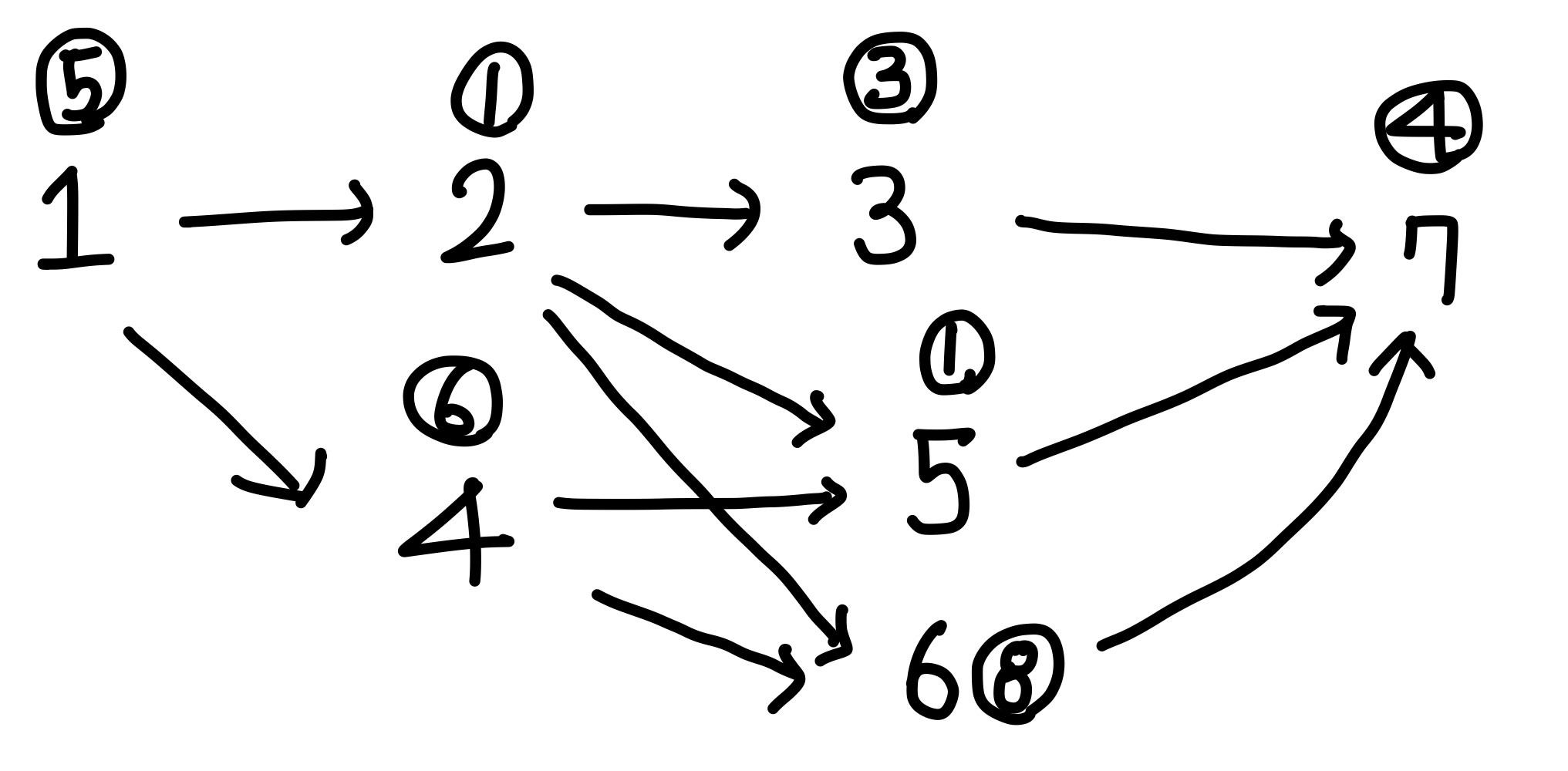
문제에서 주어진 예시를 통해 살펴보면, 1이 level 1이라고 한다면, 2와 4가 level 2, 3과 5와 6이 level 3, 7이 level 4라고 볼 수 있다.

그리고 각 레벨에서 제일 오래 걸리는 작업을 선택해서 그 값들을 모두 더하면 모든 작업을 완료하는데에 걸리는 총 시간이라고 생각했다.

 

하지만 대략 50%쯤에서 틀렸습니다가 떳다. 

반례를 찾다가, 같은 레벨에서 제일 큰 값이 다음 레벨과 연결되어 있지 않을 때 문제가 생기는 반례를 찾고, 이 방식으로는 안되겠다는 판단을 했다.

 

 

[DP를 이용한 풀이 - 통과]

문제에 K번 작업에 대해 선행 작업들의 번호는 모두 1 이상 (K-1) 이하이다.

해당 문구가 있기 때문에 DP를 적용할 수 있다.

위상 정렬을 진행하면서 현재 정점과 연결되어 있는 정점을 방문할 때에

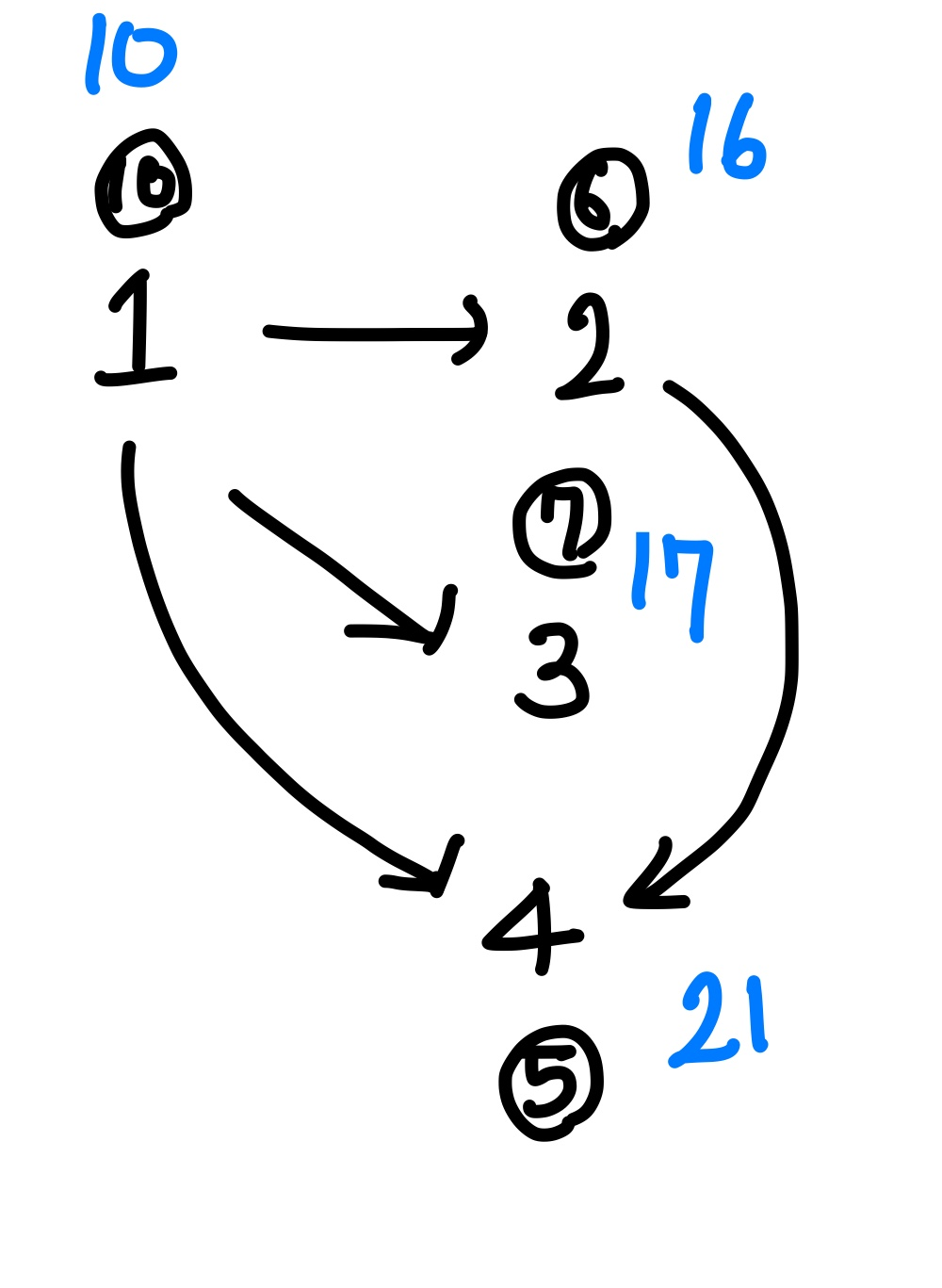
여태까지 소요된 시간(dp[cur]) + 다음 정점에서 소요되는 시간 값(requireTime[next])과 이전에 저장되어 있던 다음 정점까지의 소요되는 시간 값(dp[next]) 중에 더 큰 값을 취한다.

dp[next] = max(dp[next], dp[cur] + requireTime[next]);

 

이해가 잘 안된다면 밑의 사진을 참고하자.

 

[전체 알고리즘]

1. input을 받으면서 변수 graph, inDegree, requireTime를 갱신한다.

2. 위상 정렬을 시작하기 전에 inDegree가 0인(진입 차수가 0인) 정점들을 queue에 삽입한다.

   이 때, 해당 작업의 소요시간을 dp에 저장한다.

3. n번 반복하면서 현재 정점과 연결되어 있는 간선들의 dp값을 갱신해준다.

  dp[next] = max(dp[next], dp[cur] + requireTime[next]);

4. 위상 정렬을 진행하면서 dp의 최대 값을 결과 값(출력 값)에 저장한다.

5. 위상정렬이 끝나면 결과 값을 출력한다.

 

 

---

⭐️ Code

#include <iostream>
#include <algorithm>
#include <string>
#include <cstring>
#include <cmath>
#include <vector>
#include <queue>

using namespace std;

// 2056 - 작업
int n, result = 0;
vector<int> inDegree, requireTime, dp;
vector<vector<int>> graph;


void input(){
    cin >> n;
    inDegree.assign(n + 1, 0);
    requireTime.assign(n + 1, 0);
    dp.assign(n + 1, 0);
    graph.assign(n + 1, vector<int> (0, 0));

    for(int cur = 1; cur <= n; cur++){
        int cost, num;
        cin >> cost >> num;
        requireTime[cur] = cost; // 필요한 작업 시간
        inDegree[cur] = num; // 현재 작업의 선행 작업 개수

        for(int i = 0; i < num; i++){
           int pre;
           cin >> pre;
           graph[pre].emplace_back(cur);
        }
    }
}

void topology_sort(){
    queue<int> q;
    for(int i = 1; i <= n; i++){
        if(inDegree[i] == 0){
            q.push(i);
            dp[i] = requireTime[i];
        }
    }

    for(int i = 1; i <= n; i++){
        if(q.empty())   return;

        int cur = q.front();
        result = max(result, dp[cur]);
        q.pop();

        for(int k = 0; k < graph[cur].size(); k++){
            int next = graph[cur][k];
            dp[next] = max(dp[next], dp[cur] + requireTime[next]);
            if(--inDegree[next] == 0){
                q.push(next);
            }
        }
    }
}

int main(){

    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    input();
    topology_sort();
    cout << result;

    return 0;
}