⭐️ Topology Sort (위상 정렬)이란?
- "순서가 정해져 있는 작업"을 차례로 수행해야 할 때, 그 순서를 정렬하기 위해 사용
- 자료구조 queue를 이용해서 구현 가능
- 위상 정렬이 가능한 조건 : DAG
DAG란?
Directed Acyclic Graph의 약자로써, 사이클이 존재하지 않는(Acyclic) 방향이 있는(Directed) 그래프(Graph)이다.
만일 사이클이 있는 그래프라면 위상 정렬을 할 때 시작점을 설정할 수 없으므로 위상 정렬을 수행할 수 없다.
- Time complexity : O(V+E)
V: 정점의 개수, E: 간선의 개수
⭐️ 변수 설명
1. int v
정점의 개수를 뜻한다.
이 정보를 통해서 다른 변수의 메모리 공간을 미리 할당할 수 있다.
2. vector<int> inDegree
각 정점의 진입차수(각 정점에 꽃히는 간선의 개수)를 저장하는 변수이다.
이전에 입력받은 정점의 개수를 통해 미리 메모리 공간을 할당함으로써 메모리 공간을 아낄 수 있다.
inDegree.assign(v + 1, 0); // 입력을 받기 전에는 모든 정점의 진입 차수 : 0이후 간선 정보를 입력받으면서 간선이 꽃히는 쪽의 진입차수를 올려준다.
int start, end; // 간선의 시작 정점, 끝 정점
cin >> start >> end;
inDegree[end]++; // 간선이 꽃히는 정점에 진입차수를 올려준다.
3. vector<vector<int>> graph
Graph를 표현하는 방법 중 "인접 리스트"를 위한 변수이다.
이중 벡터를 사용함으로써 메모리가 필요한 만큼만 할당해서 사용할 수 있으며, 유동적으 사용이 가능하다.
입력받은 정점의 개수를 활용하여 .assign()함수를 통해 필요한만큼 할당한다.
// assign 함수를 통해서 vector<int>를 v+1개 할당
graph.assign(v + 1, vector<int>(0, 0));
이후 간선이 연결하는 두 정점을 입력 받으면서, 간선 정보를 graph에 입력한다.
양방향 간선이 아닌, 단방향 간선이기 때문에 간선 입력을 한 번만 한다.
int s, e;
cin >> s >> e; // s : 2, e : 5 일 때
graph[s].emplace_back(e); // graph[2].emplace_back(5);
4. queue<int> q
위상 정렬을 하기 위해 필요한 자료구조로써, 진입 차수가 0인 정점들을 큐에 넣는다.
위상 정렬을 진행하면서 queue에서 원소를 하나씩 꺼내서 해당 정점을 방문한다.
⭐️ Topology Sort (위상 정렬)의 진행 단계
1. 입력을 받으면서 진입 차수와 그래프 간선 정보를 입력한다.
2. 진입 차수(inDegree)가 0인 정점들을 queue에 push한다.
3. queue에서 원소를 하나 꺼내고, 해당 원소를 현재 방문 노드로 설정한다.
4. 현재 방문 노드와 인접한 정점들과 연결되어있는 간선을 제거한다.
따라서 인접한 정점들의 진입 차수를 1씩 줄여준다. 만일 그 이후 진입 차수가 0이 되었다면 queue에 push한다.
5. 3~4번의 과정을 반복한다.
만일 모든 정점을 방문하기 전에 queue에 빈다면 사이클이 존재한다는 뜻이다.
만일 모든 정점을 방문했다면, queue에서 꺼낸 순서(즉 방문한 순서)가 위상 정렬의 결과이다.
⭐️ Topology Sort (위상 정렬) 실행 과정
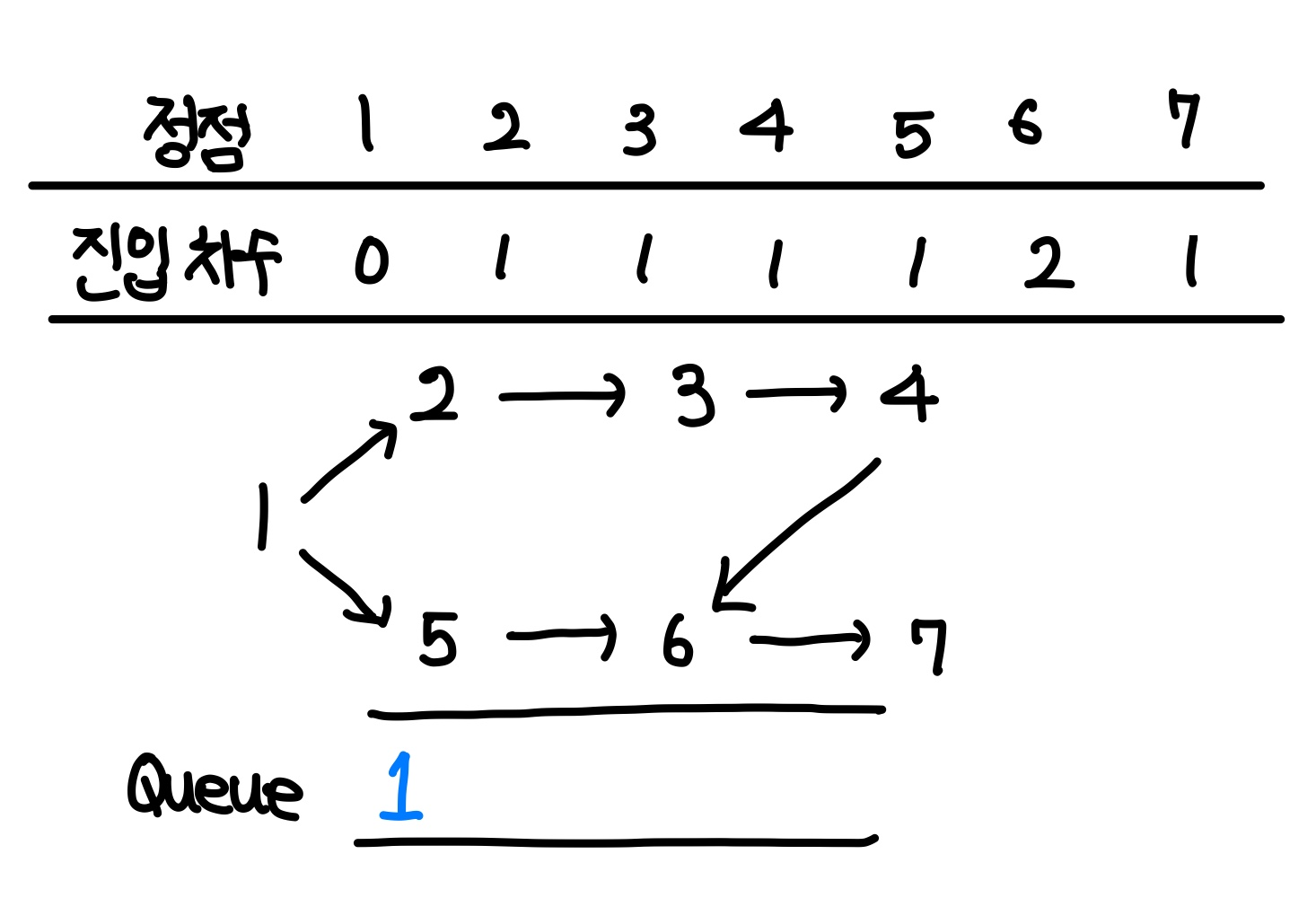
그림 1과 같은 그래프를 input에서 받았다고 가정해보자.
간선 정보를 받으면서 진입 차수도 함께 입력하기 때문에 위의 표처럼 설정이 될 것이다.
이후에 위상 정렬을 시작하기 전에 진입 차수가 0인 정점들을 queue에 넣는다.
위의 그래프에서는 진입 차수가 0인 정점은 1밖에 없으므로 queue에 1을 push 한다.
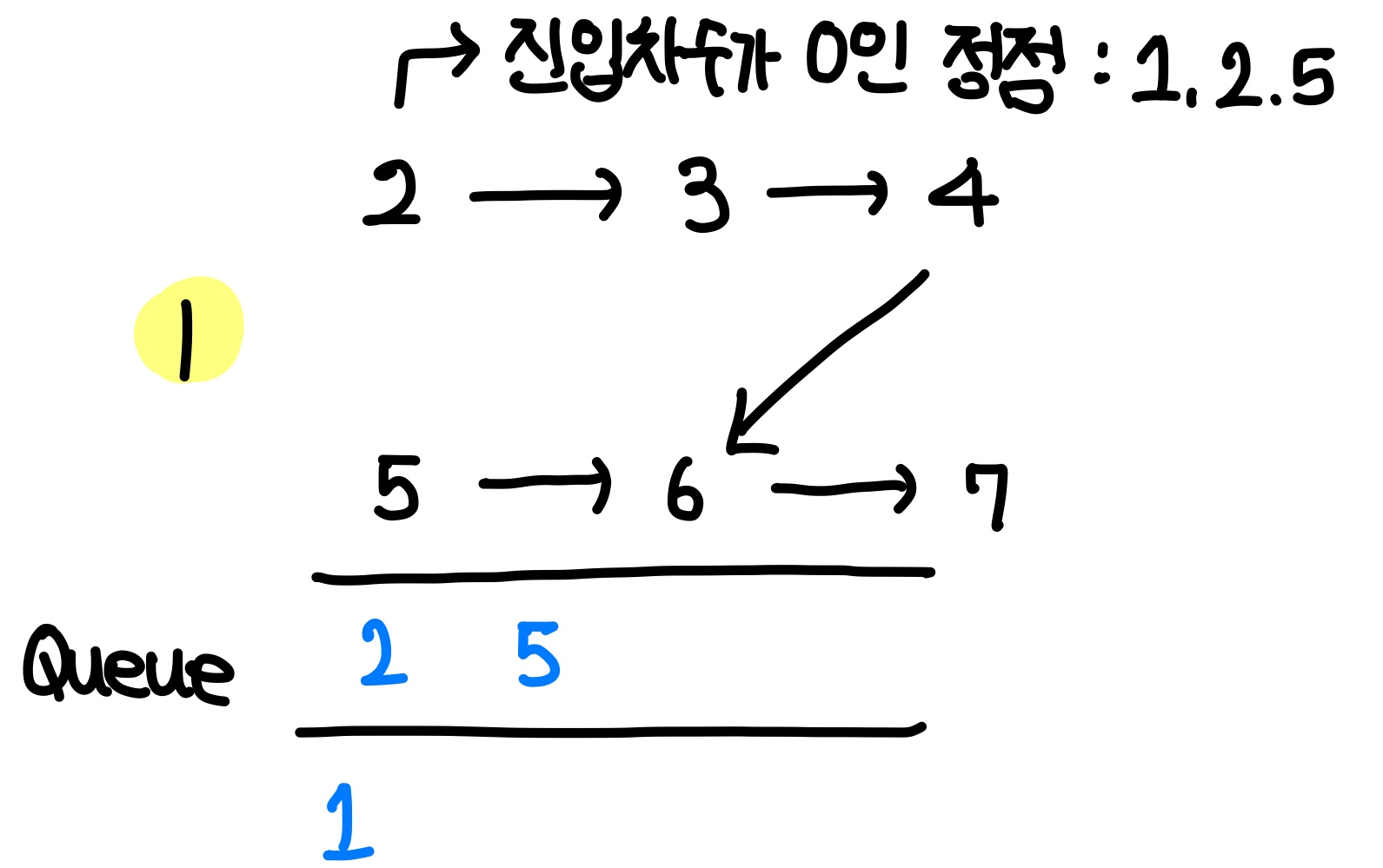
queue에서 원소를 하나 pop하여 현재 방문 정점으로 설정한다. 이번 방문 정점은 1이다.
다음에 할 일은 1에서 다른 정점으로 이어지는 간선을 제거하고, 진입 차수가 0인 정점들을 queue에 삽입하는 것이다.
1과 인접한 정점을 살펴보면 2와 5이다. 따라서 2와 5의 진입 차수를 하나 낮춰준다.
이 때, 2와 5의 진입 차수가 0이 되므로 즉시 queue에 삽입한다.
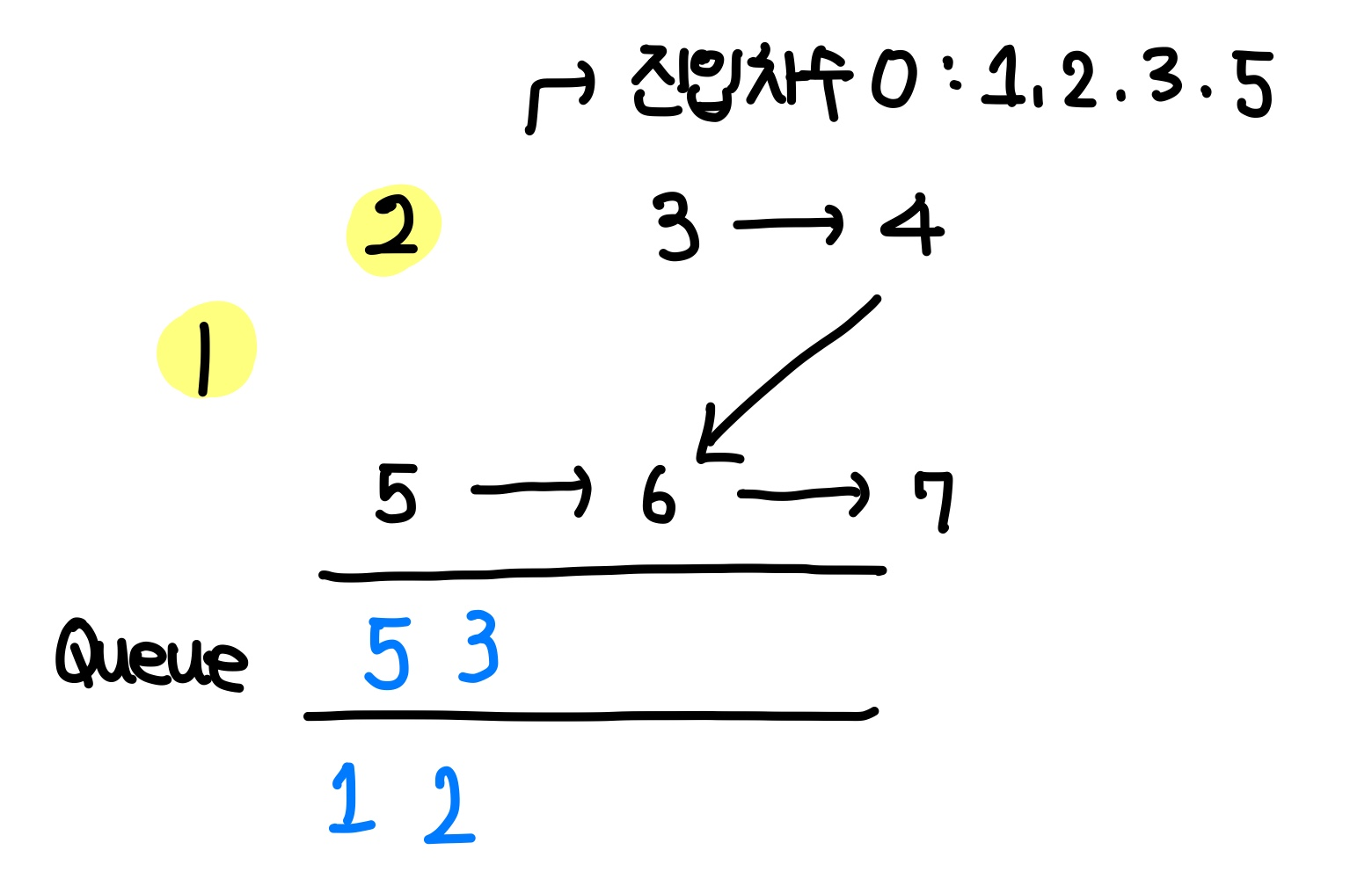
queue에서 다시 원소를 하나 pop하여 현재 방문 정점으로 설정한다. 이번에 방문하는 노드는 2이다.
위에서 했던 과정과 같이 2에서 다른 정점으로 이어지는 간선을 제거하고, 진입 차수가 0인 정점들을 queue에 삽입한다.
2와 인접한 정점은 3이기 때문에, 3의 진입 차수를 하나 낮춰준다.
이 때, 3의 진입 차수가 0이 되기 때문에 즉시 queue에 삽입한다.
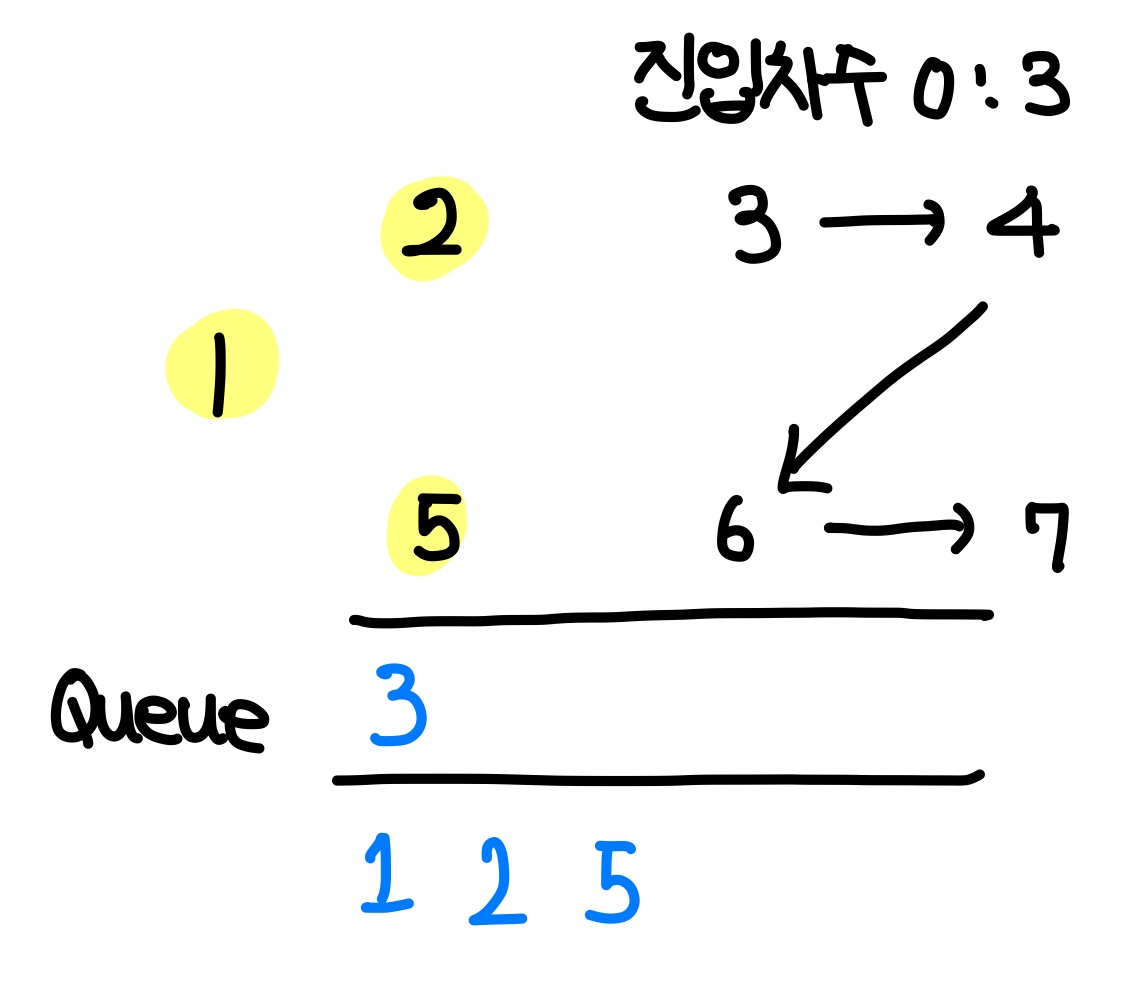
queue에서 원소를 하나 pop하여 현재 방문 정점으로 설정한다. 이번에 방문하는 노드는 5이다.
5에서 이어지는 간선은 6이므로, 6의 진입 차수를 1 내려준다.
하지만 6의 진입 차수는 0이 아닌 1이므로 아무 액션을 취하지 않고 넘어간다.
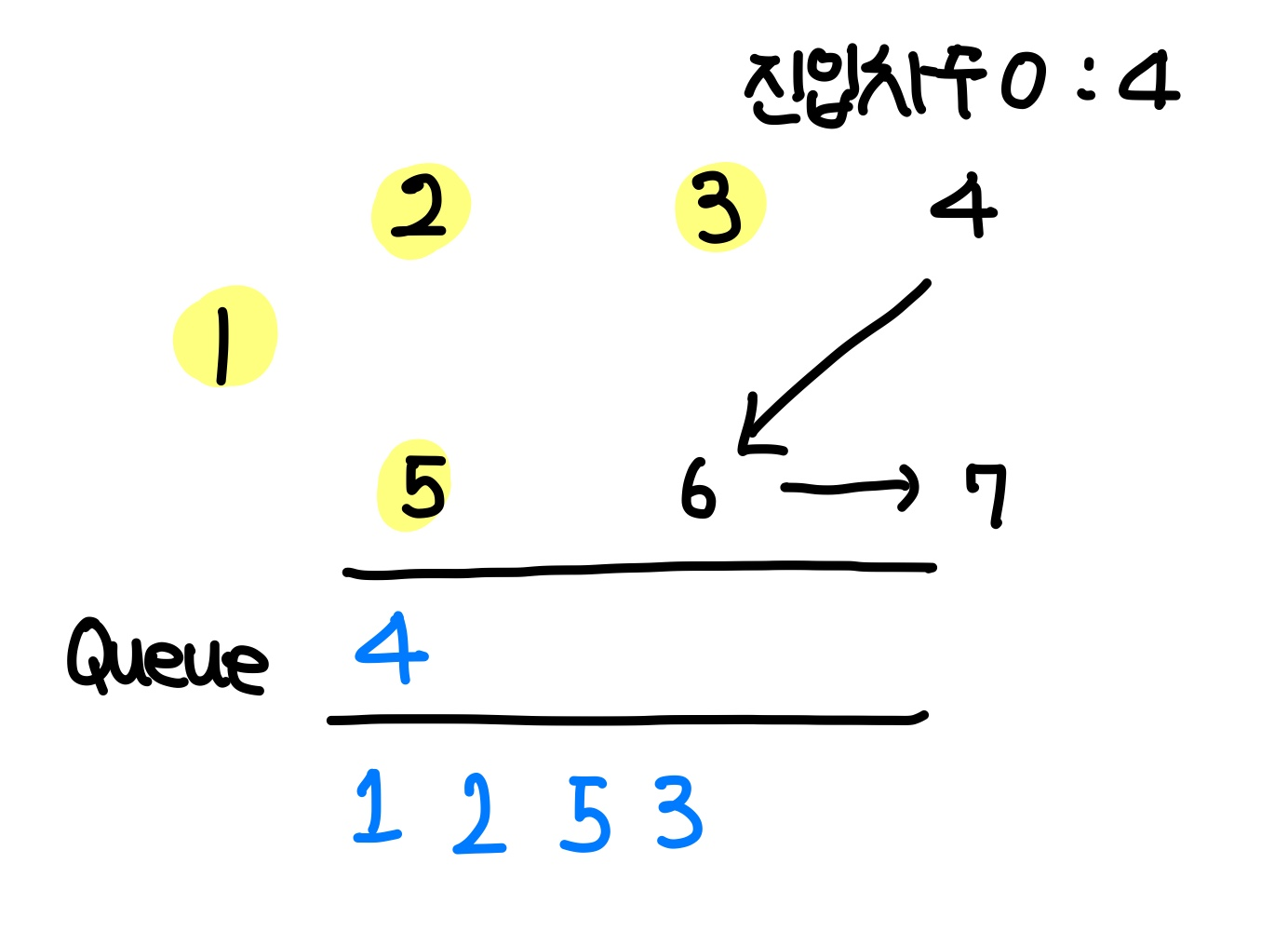
queue에서 원소를 하나 pop하여 현재 방문 정점으로 설정한다. 이번에 방문하는 노드는 3이다.
3에서 이어지는 간선은 4이므로, 4의 진입 차수를 1 내려준다.
이 때, 4의 진입 차수가 0이 되기 때문에 queue에 삽입한다.
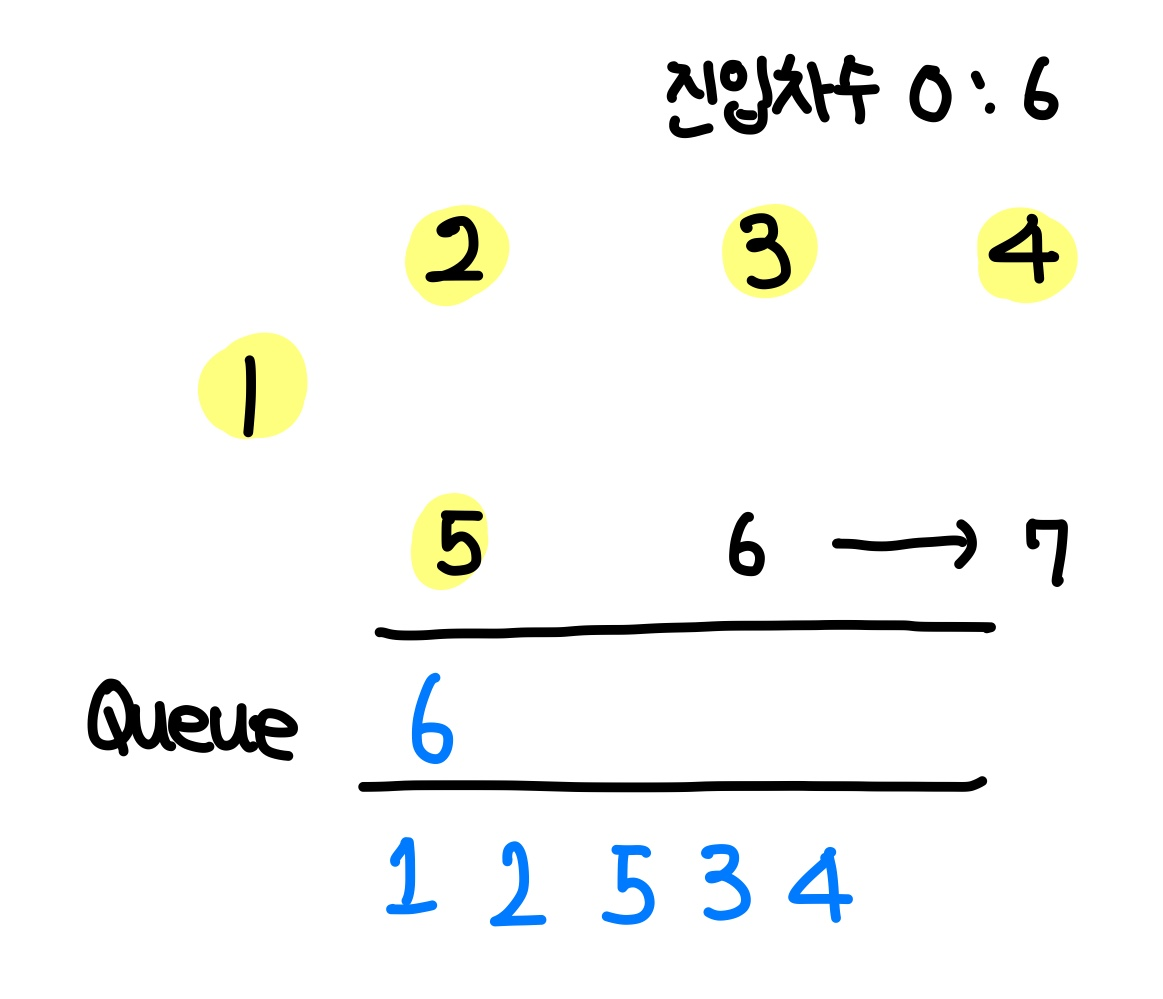
queue에서 원소를 하나 pop하여 현재 방문 정점으로 설정한다. 이번에 방문하는 노드는 4이다.
4에서 이어지는 간선은 6이므로, 6의 진입 차수를 1 내려준다.
6의 진입 차수가 0이 되었기 때문에 queue에 6을 삽입한다.
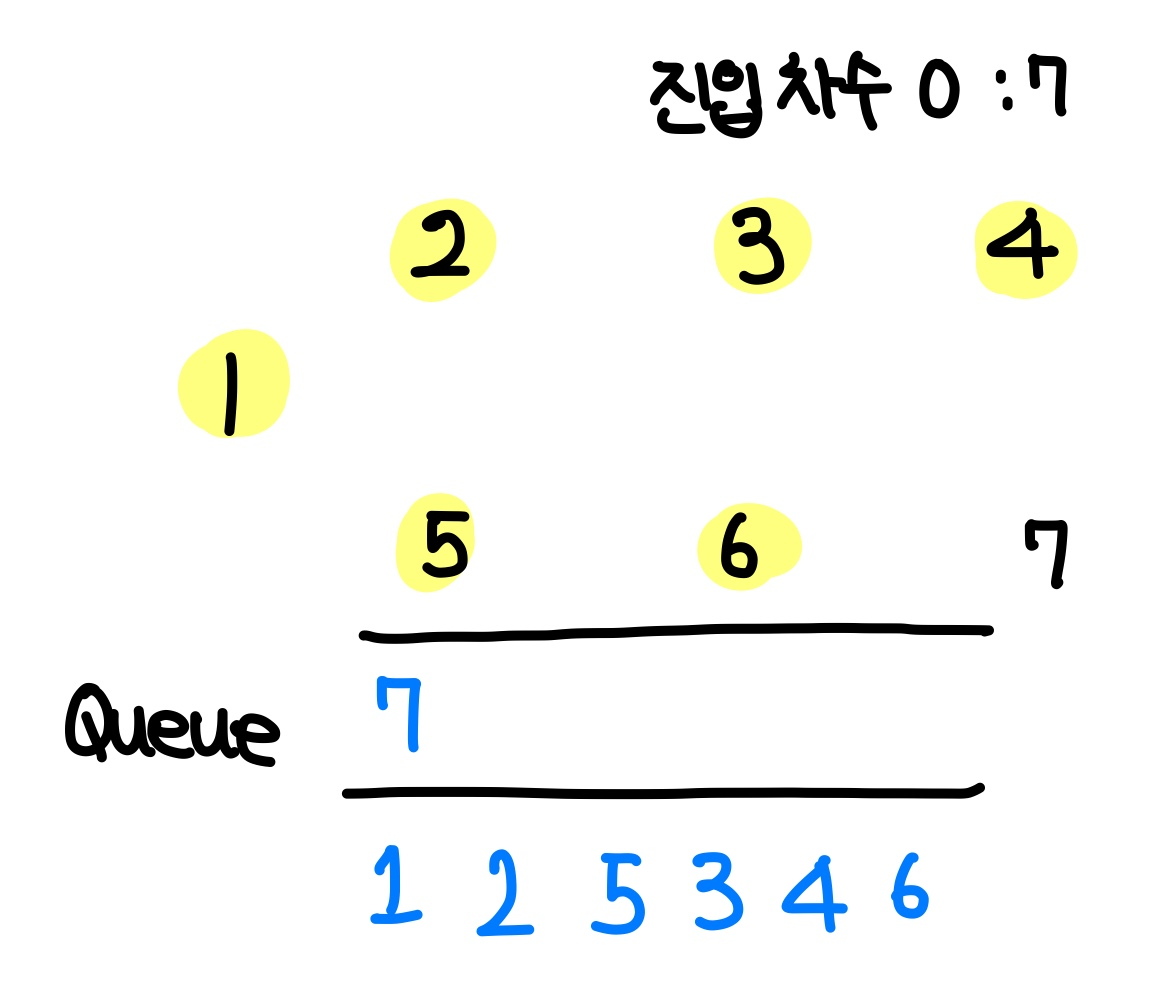
queue에서 원소를 하나 pop하여 현재 방문 정점으로 설정한다. 이번에 방문하는 노드는 6이다.
6에서 이어지는 간선은 7이므로, 7의 진입 차수를 1 내려준다.
7의 진입 차수가 0이 되었기 때문에, queue에 7을 삽입한다.
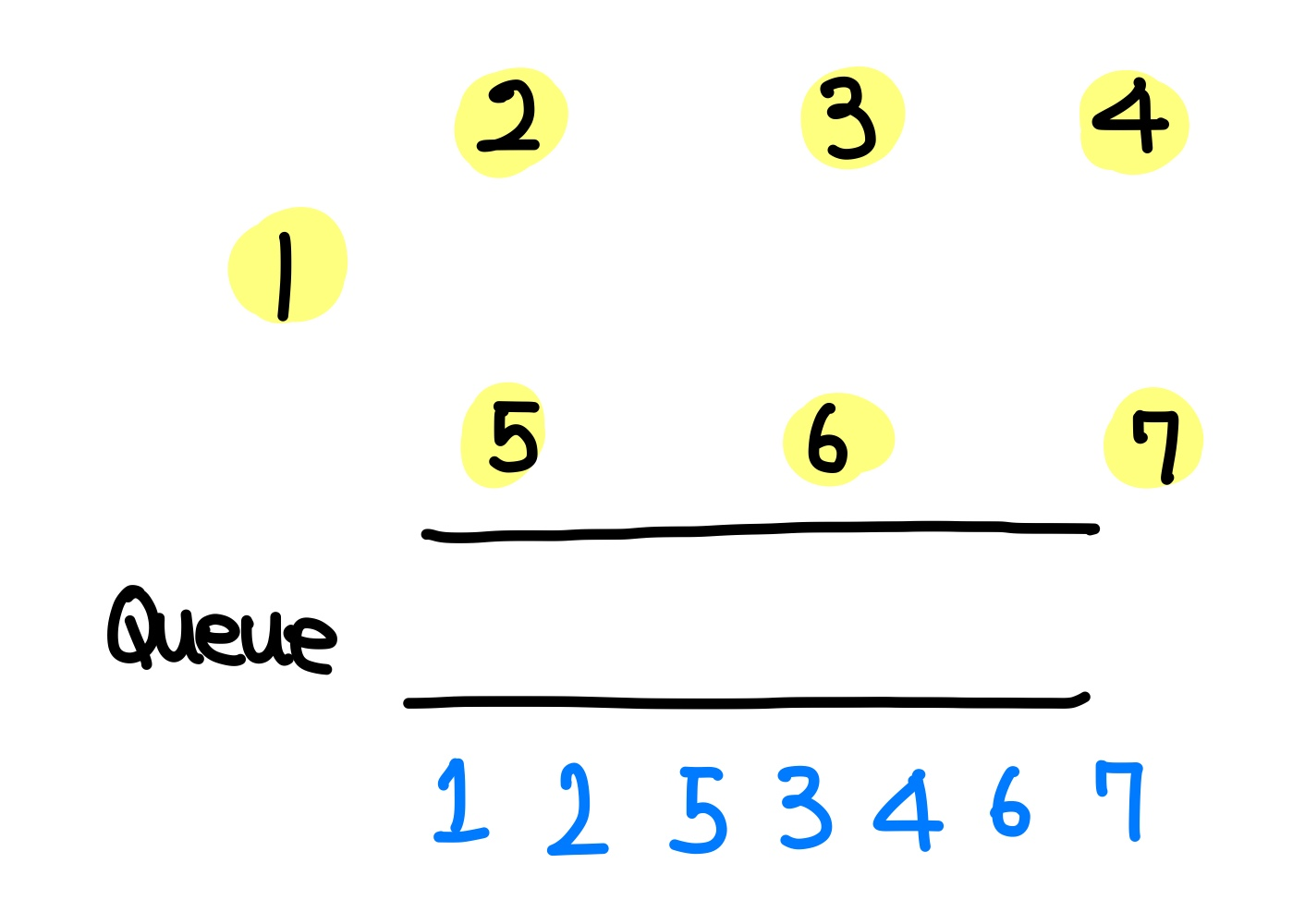
queue에서 원소를 pop하여 현재 방문 정점으로 설정한다. 이번에 방문하는 노드는 7이다.
7과 이어지는 간선이 더 이상 없으므로 queue에 아무것도 push 하지 않는다.
모든 정점을 방문하였고, queue도 비었기 때문에 위상 정렬이 종료된다.
⭐️ Code
[Parameters]
int n; // 정점의 개수
vector<int> inDegree; // 진입 차수 저장
vector<vector<int>> graph; // 간선 정보 저장
queue<int> q; // 위상 정렬을 위한 큐
[Method]
void input(){
cin >> n;
for(int i = 0; i < n; i++){
int s, e;
cin >> s >> e;
graph[s].emplace_back(e);
inDegree[e]++; // 진입 차수 +1
}
}
void topology_sort(){
// 위상 정렬을 시작하기 전에 진입 차수가 0인 정점들을 큐에 삽입한다.
for(int cur = 1; cur <= n; cur++){
if(inDegree[cur] == 0) q.push(cur);
}
// 총 n번 실행
for(int i = 0; i < n; i++){
// n번 실행하기 전에 queue가 비면 사이클이 발생했다는 뜻이다.
if(q.empty()){
cout << "cycle 발생\n";
return;
}
// queue에서 뽑아서 현재 방문 노드로 설정
int cur = q.front();
q.pop();
cout << "방문 노드 : " << cur << '\n';
// 인접한 노드들을 확인하며 진입 차수를 1씩 줄여주고, 만일 진입 차수가 0이라면 queue에 삽입한다.
for(int k = 0; k < graph[cur].size(); k++){
int next = graph[cur][k];
if(--inDegree[next] == 0) q.push(next);
}
}
}